- معايير توازن الساكنة من خلال:+ مفهوم الساكنة+ المحتوى الجيني للساكنة (Le pool de gènes)+ قانون Hardy و Weinberg وبعض تطبيقاته في حالة انتقال زوج من الحليلات- عوامل تغير الساكنة وتأثيرها على بنية الساكنة+ الطفرات+ الانتقاء الطبيعي+ الانحراف الجيني (La dérive génique)+ الهجرة (Migration)- المعايير المميزة للنوع- تعريف النوع |
1 ـ تعريف وأهداف وراثة الساكنة:
وراثة الساكنة هي جزء من علم الوراثة ، تهتم بدراسة قوانين توزيع المورثات و الأنماط الوراثية و كذا الآليات المحددة للتغير الوراثي داخل ساكنة معينة، لها ثلاثة أهداف رئيسية:
ـ قياس التغير الوراثي انطلاقا من تردد حليلات نفس المورثة.
ـ فهم كيفية انتقال التغير الوراثي من جيل لآخر .
ـ فهم آليات تطور هذا التغير الوراثي حسب الأجيال.
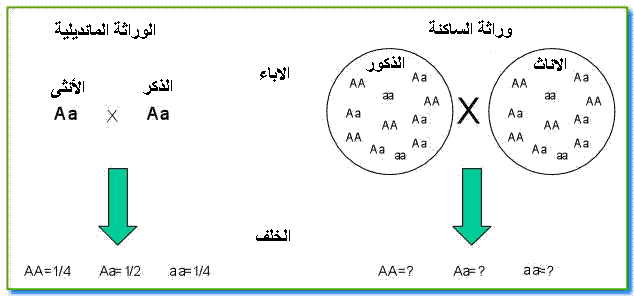
إذا كانت الوراثة المانديلية تعتمد على التزاوجات الموجهة عن طريق التجربة فان وراثة الساكنة تدرس نسب الأنماط الوراثية عند مجموعة من الأفراد ينحدرون من تزاوجات غير موجهة لعدة آباء. فهي تطبيق للوراثة المانديلية على مستوى الساكنة.
 |
2 ـ تعريف الساكنة:
الساكنة هي مجموعة من الأفراد من نفس النوع يعيشون في مجال جغرافي معين و قادرين على التزاوج فيما بينهم .
و من تم فمفهوم الساكنة يستحضر عدة معايير مكانية و زمانية و وراثية .
3 ـ المحتوى الجيني للساكنة:
3ـ1ـ ترددات المظاهر الخارجية:
عندما تكون ساكنة متعددة المظاهر الخارجية بالنسبة لصفة معينة يمكن حساب تردد المظاهر الخارجية الملاحظة.
مثال:ساكنة عدد أفرادها N حيث Nn لهم جسم أسود و Nb لهم جسم أبيض،ترددات المظاهر الخارجية بالنسبة لصفة لون الجسم هي:
ـ تردد المظهر الخارجي الأسود هو : f[n] = Nn/N
ـ تردد المظهر الخارجي الأبيض هو : f[b] = Nb/N
لكن الصعوبة تكمن في حساب ترددات الأنماط الوراثية و الحليلات.
3ـ2ـ ترددات الحليلات و الأنماط الوراثية:
مثال : في حالة مورثة غير مرتبطة بالجنس توجد على شكل حليلين A و a بحيث الحليل A سائد و يعطي اللون الأسود والحليل a متنحي و يعطي اللون الأبيض.
الأنماط الوراثية AA و Aa تعطي مظهرا أسودا في حين النمط الوراثي aa يعطي مظهرا أبيضا، إذن فحساب تردد المظاهر الخارجية لا يمكن أن يحدد لنا سوى تردد النمط الوراثي aa بما أننا لا يمكننا التمييز بين النمطين الوراثيين AA و Aa عند الأفراد ذوي اللون الأسود، و من تم صعوبة حساب ترددات الأنماط الوراثية AA و Aa وترددات الحليلات Aوa .
يمكننا حساب هذه الترددات في حالة تساوي السيادة:
مثال : في حالة مورثة غير مرتبطة بالجنس توجد على شكل حليلين B و R متساويي السيادة(تعطي مظاهر بيضاء،وردية،حمراء). يمكن إذن تحديد ترددات الأنماط الوراثية BB و BR و RR بما أنها تطابق ترددات المظاهر الخارجية.
إذا اعتبرنا ساكنة عدد أفرادها N تتوفر على :
ـ NB فرد ذو لون أبيض.
ـ NBR فرد ذو لون وردي.
ـ NR فرد ذو لون أحمر.
فان ترددات الأنماط الوراثية يحسب على الشكل التالي:
f(BB) = NB/N = D
f(BR) = NBR/N= H
f(RR) = NR/N = R
بحيث N = NB + NBR + NR
يمكن أيضا حساب ترددات الحليلات .
يكون تردد الحليل R هو حاصل عدد الحليلات R في الساكنة على مجموع حليلات المورثة في نفس الساكنة أي 2N بالنسبة لساكنة تحتوي على N فرد ثنائي الصيغة الصبغية، و تردد الحليل B هو حاصل عدد الحليلات B في الساكنة على مجموع حليلات المورثة في نفس الساكنة أي 2N .
لدينا:
NRR فرد يحتوي على حليلين R
NRB فرد يحتوي على حليل R و حليل B
NBB فرد يحتوي على حليلين B
عدد الحليلات R في الساكنة هو 2NRR + NRB
عدد الحليلات B في الساكنة هو 2NBB + NRB
إذن ترددات الحليلات R و B هي :
f(R) = p = (2 NRR+ NRB)/2N = NRR/N + NRB/2N
f(B )= q = (2NBB+ NRB)/2N = NBB/N + NRB/2N
مع p + q = 1
بصيغة أخرى إذا كانت D و R تمثل على التوالي ترددات الأنماط الوراثية متشابهة الاقتران RR و BB و H تردد النمط مختلف الاقتران RB فان ترددات الحليلات تحسب انطلاقا من ترددات الأنماط الوراثية على الشكل التالي:
f(R) = p = D + H/2
f(B) = q = R + H/2
هذه الترددات p و q تمثل أيضا احتمال أن يحمل مشيج (ذكري أو أنثوي) الحليل R أو الحليل B .
تجدر الإشارة إلى أن ترددات الحليلات لا تعطي فكرة حول نمط اقتران الحليلات عند الأفراد عكس ترددات الأنماط الوراثية التي تعطي فكرة واضحة حول طبيعة اقتران الحليلات مثنى مثنى.
4 ـ قانون Hardy-Weinberg1908
Hardy : عالم رياضيات انجليزي
Weinberg : طبيب ألماني
4ـ1ـ الساكنة النظرية المثالية:
ترجع صعوبة تتبع التغير الوراثي لساكنة عبر الأجيال إلى عدة عوامل يمكنها تغيير ترددات الحليلات نذكر منها الطفرات ، الهجرات اختلاف مدة عيش و خصوبة الأفراد... لهذا نعتمد على تتبع الخاصيات الوراثية بالنسبة لساكنة نظرية مثالية التي تتميز بالخصائص التالية:
ـ ساكنة مكونة من كائنات ثنائية الصيغة الصبغية ذات توالد جنسي و أجيال غير متراكبة(غياب التزاوج بين أفراد من أجيال مختلفة).
ـ ساكنة ذات عدد غير محدود و تزاوجات عشوائية و بالصدفة( لا يتم اختيار الشريك الجنسي بل بتم التزاوج بالصدفة أيضا التقاء الأمشاج يكون بالصدفة)
ـ ساكنة مغلقة وراثيا ( غياب الهجرة).
ـ لجميع أفراد الساكنة القدرة على التوالد و إعطاء خلف قادر على العيش (غياب الانتقاء)
ـ غياب الطفرات و شذوذات الانقسام الاختزالي أثناء تشكل الأمشاج.
4ـ2ـ قانون Hardy-Weinberg:
يشكل هذا القانون نموذج مرجعي في علم وراثة الساكنة، و يعتبر أن ترددات الحليلات و ترددات الأنماط الوراثية تبقى مستقرة من جيل لآخر نقول حين إذن أن الساكنة في توازن .
أ ـ حالة انتقال مورثة غير مرتبطة بالجنس ذات حليلين A و a :
إذا اعتبرنا أن ترددات الأنماط الوراثية AA وAa وaa هي نفسها عند الجنسين:
تردد AA هو D و تردد aa هو R و تردد Aa هو H بحيث H+D+R=1
ـ ترددات الحليلات في الجيل G0 هي :
بالنسبة للحليل A :
f(A) = p0 = D0 + H0/2
بالنسبة للحليل a :
f(a) = q0 = R0 + H0/2
مع p0 + q0 = 1
ـ ترددات الحليلات في الجيل G1 هي :
في ساكنة نظرية مثالية تمثل هذه الترددات p0 و q0 أيضا ترددات الأمشاج التي تحمل على التوالي الحليل A و الحليل a .
و بما أن التزاوج يتم بالصدفة فان تكون الجيل G1 ينتج عن طريق التقاء مشيج ذكري يحمل الحليل A أو a بتردد p0 أو q0 و مشيج أنثوي يحمل الحليل A أو a بتردد p0 أو q0
| A (p0) | a (q0) | |
| A (p0) | AA (p02) | Aa (p0q0) |
| a (q0) | Aa (p0q0) | aa (q02) |
إذن ترددات الأنماط الوراثية AA و Aa و aa تحسب على الشكل التالي:
f(AA) = p02 =D1
f(Aa) = 2p0q0 =H1
f(aa) = q02 =R1
تردد الحليل A في الجيل G1 هو :
f(A) = p1=D1+H1/2=p02 +2p0q0 /2=p02 +p0q0=p0(p0+q0)
و بما أن p0 + q0 = 1 فان f(A)=p1=p0
تردد الحليل a في الجيل G1 هو :
f(a)=q1=R1+H1/2=q02 +2p0q0 /2=q02 +p0q0=q0(q0+p0)
و بما أن p0 + q0 = 1 فان f(a)=q1=q0
و بالتالي فترددات الحليلات لم تتغير و من تم الحصول في الجيل الموالي G2 على نفس ترددات الأنماط الوراثية :
ـ P2 بالنسبة للنمط الوراثي AA .
ـ 2pq بالنسبة للنمط الوراثي Aa .
ـ q2 بالنسبة للنمط الوراثي aa .
أي هناك استقرار في ترددات الحليلات و ترددات الأنماط الوراثية،و هذا ما يعرف بتوازن Hardy-Weinberg .
و تمثل ترددات الأنماط الوراثية نشر للحدانية 2(p+q) أي p2 + 2pq + q2
العلاقة بين ترددات الحليلات و ترددات الأنماط الوراثية يمكن تمثيلها حسب الوثيقة التالية:
نلاحظ انه عندما تكون p=q=0,5 تكون ترددات الأنماط الوراثية f(AA) =1/4 و f(Aa) =1/2 و f(aa) =1/4 و هي نفس ترددات الأنماط الوراثية في الوراثة المانديلية عند تزاوج فردين مختلفي الاقتران،و هي تمثل حالة خاصة لقانون Hardy-Weinberg .
ـ تمرين:
تتحكم في لون احد انواع الفراشات مورثة على شكل حليلين C سائد و يعطي اللون القاتم و c متنحي و يعطي اللون الفاتح.
اذا اعتبرنا ساكنة متوازنة حيث تردد الفراشات القاتمة هو 0.98 ,حدد تردد الحليلات C و c في هذه الساكنة.
ب ـ حالة انتقال مورثة متعددة الحليلات(n حليل):
يطبق قانون Hardy-Weinberg أيضا على المورثات متعددة الحليلات، بحيث إذا كانت ترددات مختلف الحليلات على التوالي p1 و p2 و p3 ...و pn فان ترددات مختلف الأنماط الوراثية هي نشر للحدانية 2(p1+p2+ p3 + ...+ pn) أي
p12 p22 p32 ....pn2 2p1p2 2p1p3...2p1pn 2p2p3...2p2pn 2p3pn .......
مثال: نظام الفصائل الدموية ABO عند الإنسان.
هناك 3 حليلات A و B و O بترددات على التوالي p و q و r
في حالة ساكنة متوازنة حسب قانون H-W تكون ترددات الأنماط الوراثية بعد نشر الحدانية 2(p+q+ r) على الشكل التالي:
p2 AA q2 BB r2 OO 2pq AB 2pr AO 2qr BO
ج ـ حالة مورثة مرتبطة بالجنس ذات حليلين A و a:
اذا اعتبرنا ساكنة متوازنة حيث تردد الحليلات متساو عند الجنسين سيكون لدينا:
ـ عند الذكور: ترددات الأنماط الوراثية XAY و XaY هي نفسها ترددات الحليلات A و a على التوالي p و q
ـ عند الاناث: ترددات الأنماط الوراثية XAXA و XaXA و XaXa هي على التوالي p2 و 2pq و q2
| XA (p) | Xa (q) | Y | |
| XA (p) | XAXA (p2) | XAXa (pq) | XAY (p) |
| Xa (q) | XAXa (pq) | XaXa (q2) | XaY (q) |
| الحصيلة | انثى | ذكر | |||
| غير مصابة | مصابة | غير مصاب | مصاب | ||
| q> q2 الاناث اقل اصابة من الذكور | p2 +2pq | q2 | p | q | حالة حليل متنح |
| p2 +2pq>p الاناث اكثر اصابة من الذكور | q2 | p2 +2pq | q | p | حالة حليل سائد |
5 ـ تطبيق قانون Hardy-Weinberg
ـ اختبار التوازن:
يرتكز قانون Hardy-Weinberg على استدلال مبني على الاحتمالات و بالتالي لا يمكن تطبيقه عادة إلا على ساكنة ذات عدد غير محدود و تخضع لمجموعة من الشروط الغير متوفرة دائما في الطبيعة (غياب الطفرات،غياب الهجرة،غياب الانتقاء...) ، من جهة أخري يسهل تطبيقه في حالة تساوي السيادة حيث من الممكن حساب ترددات الحليلات انه اختبار التوازن.
يمكن اختصار مبدأ هذا الاختبار في ثلاث مراحل:
1 ـ أخذ عينة من الساكنة و جرد الأعداد الحقيقية للأنماط الوراثية (هذا ممكن نظرا لتساوي السيادة) و حساب الترددات الحقيقية للحليلات من بين N فرد تم جرده.
f(A) = p
f(a) = q
2 ـ حساب أعداد الأنماط الوراثية المتوقعة لساكنة نظرية مثالية لها نفس عدد و ترددات حليلات الساكنة المدروسة، أي:
AA = p2 x N Aa = 2pq x N aa= q2 x N
3 ـ مقارنة الأعداد الملاحظة Eo والأعداد النظرية Et بواسطة اختبار إحصائي Χ2 (كي اثنان khi deux) و الذي يمكن من اختبار فرضية تطابق الأعداد الملاحظة و الأعداد النظرية(فرضية H0 ).
Χ2 = Σ(Eo - Et )2/Et
مثال: في حالة 3 أنماط و راثية RR و BB و RB يحسب Χ2 على الشكل التالي:
Χ2 = (ERRo - ERRt )2/ERRt +(EBBo - EBBt )2/EBBt +(ERBo - ERBt )2/ERBt
تقارن قيمة Χ2 المحسوبة مع قيمة عتبة تقرأ على جدول خاص (انظر مختصر هذا الجدول أسفله) بدلالة معيارين :
ـ احتمال الخطأ α و يتم اختياره من طرف المختبر و هو عادة 5% أي 0,05
ـ درجة الحرية ـ degres de liberte - ddl
ddl=NC - NPEI
عدد الأقسام NC
عدد العلاقات المستقلة بين الأقسام او المعايير التجريبية المستقلة المستعملة لحساب الاعداد المنتظرة NPEI
عدد الأقسام يمثل هنا عدد الانماط الوراثية
المعايير التجريبية المستقلة المستعملة لحساب الاعداد المنتظرة:يوجد في هذه الحالة معيارين:
المعيار الاول هو العدد الاجمالي للأفراد
المعيار الثاني هو احدى ترددات الحليلات
مثال: في حالة المثال الأخير لدينا:
عدد الاقسام ( الانماط الوراثية) هو 3
المعايير التجريبية المستقلة المستعملة لحساب الاعداد المنتظرة هو 2
و بالتالي:
ddl=3-2=1
ـ اذا كانت قيمة Χ2 المحسوبة أصغر من القيمة العتبة Χ2 في الجدول نقبل الفرضية H0 و نقول أن الساكنة تخضع لقانون Hardy-Weinberg أي في توازن.
ـ اذا كانت قيمة Χ2 المحسوبة أكبر من القيمة العتبة Χ2 في الجدول نستبعد الفرضية H0 و نقول أن الساكنة لا تخضع لقانون Hardy-Weinberg مع احتمال الخطأ يساوي 5% .
extrait du tableau |
مثال:
يحدد نظام الفصائل الدموية MN عند الإنسان من طرف مورثة على شكل حليلين M و N متساويي السيادة.
أعطت دراسة أجريت على 730 فرد من السكان الأصليين لأستراليا النتائج التالية:
22 MM 216 MN 492 NN
1 ـ حساب ترددات الحليلات M و N :
ـ بالنسبة للحليل M :
p = (22 + 1/2 x 216) / 730 = 0,178
ـ بالنسبة للحليل N :
q = 492 + 1/2 x 216) / 730 = 0,822
2 ـ حساب الأعداد النظرية المنتظرة لمختلف الأنماط الوراثية:
MM = p2 x 730 = (0,178)2 x 730 = 23,1
MN = 2pq x 730 = (2 x 0,178 x 0,822) x 730 = 213,6
NN = q2 x 730 = (0,822)2 x 730 = 493,2
3 ـ اختبار X2
X2 = (22-23,1)2/23,1 + (216-213,6)2/213,6 + (492-493,2)2/493,2 = 0,083
بالرجوع إلى الجدول وبالنسبة لدرجة حرية ddl=3-2=1 و احتمال خطأ 5% نجد أن قيمة العتبة هي 3,84
نلاحظ أن القيمة المحسوبة لـ X2 اصغر بكثير من العتبة إذن ليس هناك فرق بين النتائج الملاحظة و النتائج النظرية و نقول أن ساكنة السكان الأصليين لاستراليا تخضع لتوازن Hardy-Weinberg.
6 ـ خلاصة :
في أغلب الحالات يمكن نموذج Hardy-Weinberg من إعطاء فكرة مهمة عن البنية الوراثية للساكنات الطبيعية لان فرضية التزاوجات بالصدفة غالبا ما تحترم و تأثيرات الطفرات و الهجرة و الانتقاء ليست بالدرجة التي يمكنها إحداث اختلاف بين ترددات الأنماط الوراثية و نموذج Hardy-Weinberg و من تم يمكن استعمال هذا القانون لوضع توقعات في عدة مجالات نذكر من بينها المجال الطبي.
7 ـ عوامل التغير الوراثي:
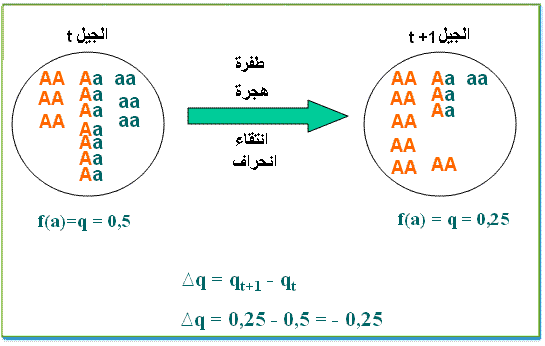
أ ـ الطفرات :
الطفرة هي كل تغير مفاجئ في المادة الوراثية تساهم في التجديد و التغير الوراثي، و يمكن تصنيفها إلى طفرات حليلية و طفرات صبغية. و لا تكون وراثية إلا إذا همت الخلايا الجنسية.
ـ أنواع الطفرات:
ـ الطفرات الحليلية: وهي طفرات مرتبطة بتغيرات في تسلسل النيكليوتيدات بسبب الاستبدال أو الإضافة أو الضياع أو الانتقال و قد تهم نيكليونيدا واحدا أو أكثر. كما يمكن مضاعفة الحليل بأكمله.
بعض الأمثلة:
الحالة العادية
|
|
طفرة صامتة لا تحدث أي تغير في طبيعة البروتين
|
|
الحالة العادية
|
|
طفرة بدون معنى توقف تركيب البروتين
Béta thalassémie
|
|
طفرة تحدث تغيرا في طبيعة البروتين
أمثلة لبعض الطفرات و عواقبها
|
http://formation.etud.u-psud.fr
انظر الوثيقة1 ـ انظر الوثيقة2 ـ انظر الوثيقة3
ـ الطفرات الصبغية: مرتبطة بتغيرات في بنية أو عدد الصبغيات الذي يؤدي إلى تعدد المظاهر.
شذوذ الانقسام الاختزالي
ـ دور الطفرات في التغير الوراثي:
تعد الطفرات ذات أهمية في انتاج اشكال جديدة من الحليلات.
لنعتبر مورثة ذات حليلين A و a بحيث تمثل u معدل الطفرة من A إلى a و v معدل الطفرة العكسية من a إلى A
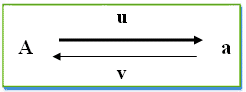
اذا اعتبرنا p0 و q0 ترددات الحليلات A و a في الجيل G0 ، فان ترددات هذه الحليلات p1 و q1 في الجيل G1 هي:
f(A) p1 = p0 - u p0 + v q0f(a) q1 = q0 - v q0 + u p0الفارق Dq لتردد الحليل a بين الجيلين G0 و G1 هو :
Dq = q1 - q0Dq= -vq0 + up0
الفارق Dp لتردد الحليل A بين الجيلين G0 و G1 هو :Dp = p1 - p0Dp= -up0 + vq0في حالة التوازن ، لا تتغير ترددات الحليلات A و a بين جيلين متتاليين (pn+1 = pn و qn+1 = qn ) أي
D q = 0 D p = 0
Dq = - v qe + u pe = 0Dq = - v qe + u (1-qe) = 0Dq = - v qe + u - uqe = 0Dq = u -qe (u + v) = 0
qe = u / (u + v)بالنسبة للحليل A :
pe= v / (u + v)اذن فقيم ترددات الحليلات في حالة التوازن ترتبط فقط بمعدلات الطفرةمثال: إذا اعتبرنا
u=10-6 فان تردد الجليل A في حالة التوازن هي
pe= v / u + v = 10-7 / 10-6 10-7
pe=0,09و من تم qe=0,91
ـ العلاقة بين نسبة الطفرات و المحتوى الجيني للساكنة:
يمثل الجدول التالي نسبة الطفرات عند بعض المتعضيات
| الكائن | تغير المظهر الخارجي | نسبة الطفرات |
| العاتية | كبح الانحلال | 10-8 |
| تعير نوعية العائل | 3.10-9 | |
| Escherichia coli | عدم القدرة على تخمر اللاكتوز | 2.10-7 |
| Chlamydomonas | streptomycine مقاومة | 10-8 |
| فطر نوروسبورا | inositol عدم القدرة على تركيب | 8.10-8 |
| ذبابة الخل | ظهور عيون بيضاء | 4.10-5 |
بما ان نسبة الطفرات ضعيفة جدا فان تغير تردد الحليلات داخل الساكنة بواسطة الطفرات يكون ضعيفا لكن مع تعدد الاجيال تصبح مهمة مما يؤدي الى تغير المحتوى الجيني للساكنة.
ـ خلاصة:
تعتبر الطفرات الظاهرة الاساسية التي تنتج عنها حليلات جديدة و بذلك ترفع من التغير الوراثي داخل الساكنات الطبيعة،و هي نادرا ما تكون مفيدة.
ب ـ الانتقاء : انظر الوثيقة1 ـ انظر الوثيقة2 ـ انظر الوثيقة3
 |  |  |
http://evolution.berkeley.edu
ـ دراسة مثال:
تعتبر أرفية البتولة فراشة ليلية تقضي النهار على جذوع الاشجار و لها مظهرين فراشات ذات لون قاتم و فراشات ذات لون فاتح.:
 |
و يمثل الجدول التالي توزيع هذه الفراشات في منطقتين منطقة صتاعية و منطقة قروية
| | منطقة صناعية | منطقة قروية | ||
| مظهر الخارجي | فاتح | قاتم | فاتح | قاتم |
| % الاشكال داخل الساكنة | 11 | 89 | 100 | 0 |
| % الأشكال المصطادة | 74 | 26 | 14 | 86 |
من خلال معطيات الجدول يتبين ان تردد الفراشات يختلف حسب المنطقة ففي المنطقة الصناعة نلاحظ ارتفاع تردد الفراشات القاتمة بينما في المنطقة القروية هناك ارتفاع في تردد الفراشات الفاتحة ، و يمكن تفسير ذلك باختلاف القدرة على التخفي من الطيور المفترسة حسب المناطق انه الانتقاء الطبيعي.
تتحكم في لون الفراشات مورثة على شكل حليلين C سائد و c متنحي. النمط الوراثي للفراشات القاتمة هو CC أو Cc و الفراشات الفاتحة cc .
يمثل الجدول التالي تغير نسب الحليلات مع توالي الاجيال في منطقة صناعية من ستة 1858 الى 1948 .
| الاجيال | 1858 | 1868 | 1878 | 1888 | 1908 | 1928 | 1938 | 1948 | |
| نسب الحليلات | C | 0 | 3 | 45 | 76 | 90 | 94 | 96 | 96 |
| c | 100 | 97 | 55 | 24 | 10 | 6 | 4 | 4 | |
نلاخظ التراجع التدريجي للحليل c و تثبيت الحليل السائد C في المنطقة الصناعية اذن هناك تغير في البنية الوراثية للساكنة.
ـ خلاصة:
ـ نتحدث عن الانتقاء الطبيعي عندما لا يكون لافراد ساكنة معينة نفس القدرة على التوالد و اعطاء خلف قادر على العيش مما يؤدي الى انتقال حليلات بعض الافراد بشكل تفاضلي الى الاجيال الموالية مسببا تغيرا في البنية الوراثية للساكنة.
ـ الانتقاء الطبيعي:يقلص عموما من التغير الوراثي داخل الساكنة عبر ازالة بعض الانماط الوراثية غير الملائمة(ويمكن أن يحافظ على بعض التنوعات الوراثية)
ـ انواع الانتقاء الطبيعي:
ـ الانتقاء المثبت: يؤدي الى حذف المظاهر الخارجية الموجودة في الطرفين
ـ الانتقاء الاتجاهي: يؤدي الى حذف المظاهر الخارجية الموجودة في احد الطرفين
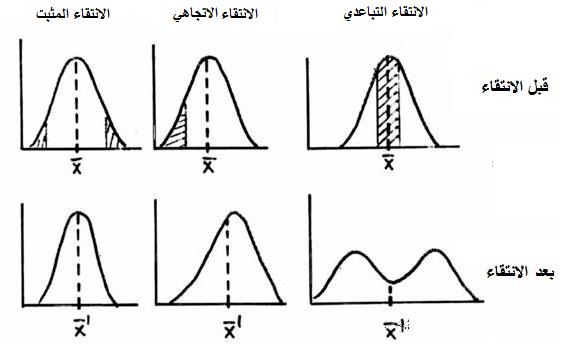
د ـ الانحراق الجيني : انظر الوثيقة1 ـ انظر الوثيقة2 ـ الوثيقة 3 ـ الوثيقة 4
http://evolution.berkeley.edu
1 ـ الكشف عن الانحراف الجيني
| télécharger puis exécuter Genpopusetup.exe (1,9 Mo). |
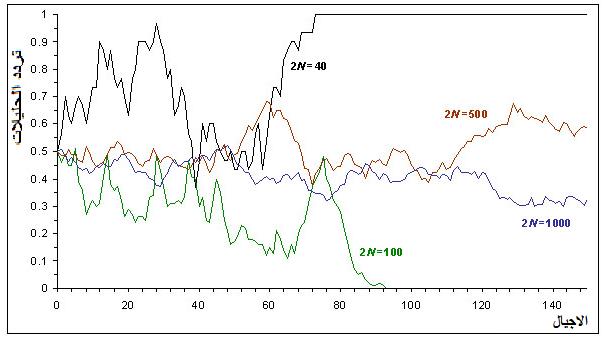
تمثل الوثيقة التالية تطور تردد الحليلات داخل 4 ساكنات تجريبية مختلفة القد.
http://lgb.unige.ch/evolution/images/GeneticDrift2.jpg
ـ في بداية التجربة : كانت ترددات الحليلات عند كل الساكنات تساوي 0,5
ـ بعد 80 جيل تقريبا يلاحظ أن ترددات الحليلات تتطور بشكل مختلف حسب قد الساكنة ففي الساكنات الصغيرة تتغير الترددات بشكل كبير بالمقارنة مع الساكنات الكبيرة، حيث يمكن اختفاء أو تثبيت بعض الحليلات مع مرور الزمن.
من تم فكلما كانت الساكنة صغيرة ستنتشر التجديدات الوراثية فيها بشكل سريع. هذه التغيرات غير منتظرة فهي عشوائية وهذا ما يعرف بالانحراف الجيني العشوائي.
ملحوظة: على عكس الانحراف الجيني، في الانتقاء الطبيعي نتوقع الحليل الذي سيثبت والذي سيختفي(مثال فراشات الأرفية)
2 ـ نمذجة للانحراف الجيني: مفعول "عنق الزجاجة" bottleneck
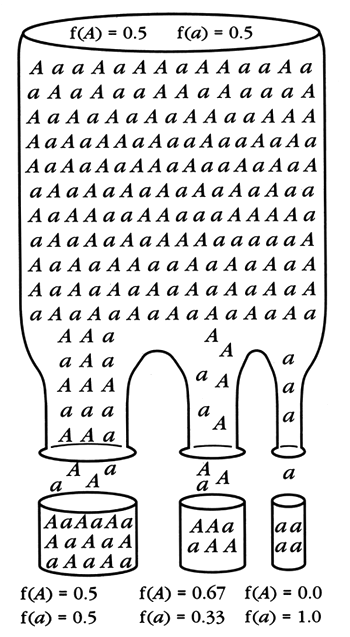
http://www.fao.org/docrep/006/x3840e/X3840E161.gif
3 ـ تعريف الانحراف الجيني:
ـ يمثل الانحراف الجيني التقلبات العشوائية لترددات الحليلات من جيل الى اخر داخل الساكنات الصغيرة و يرجع ذلك الى التعيان العشوائي من بين الأمشاج.(كلما كانت الساكنة صغيرة كان احتمال سحب امشاج من نفس النوع كبيرا)، فالمدة الزمنية الكافية لحذف او تثبيت حليل معين تنخفض كلما صغر حجم الساكنة.
ـ يقلص من التغير الوراثي داخل الساكنة باختفاء حليلات و تثبيت اخرى .
ج ـ الهجرة :
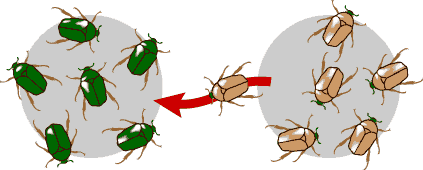
http://evolution.berkeley.edu
تؤدي الهجرة الى انتقال الحليلات عبر انتقال الافراد بين ساكنات متباعدة من نفس النوع.

اذا اعتبرنا في الجيل G0 ان ترددات الحليلات مختلفة بين الساكنتين،pm بالنسبة لساكنة المهاجرين و p0 بالنسبة للساكنة المستقبلة (الجزيرة)،
سيكون تردد الحليل A في الجيل G1 يعد تدفق هجري m هو:
p1 = (1 - m) p0 + m pm
ـ فرق ترددات الحليل
Dp= p 1- p0 = m (pm - p0)ـ اي بين جيلين t و t+1
Dp=p t+1 - pt= m (pm - pt)و بالتالي تغير ترددات الحليلات متناسب مع التدفق الهجري m و فرق التردد بين الساكتين.
اي ترددات الحليلات في الساكنة المستقبلة(الجزيرة) متساوية مع ترددات الحليلات في ساكنة المهاجرين(القارة).
pe= pmqe= qm
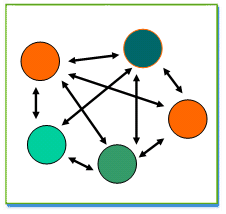
ـ نموذج الارخبيل
تبادلات متعددة الاتجاهات بين ساكنات مقسمة و موزعة على عدة مناطق(كمجموعة من الجزر). وبفعل هذا التدفق الهجري تتقلص تدريجيا الاختلافات الحاصلة في تردد الحليلات و تنحو الى تردد مشترك يقابل معدل تردد الحليلات عند هذه الساكنات.
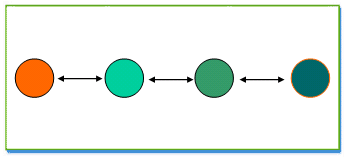
ـ النموذج الخطي: stepping stone model
مثل بنية النهر حيث تكون هجرة ساكنة المنبع في اتجاه خطي نحو المصب و تمر عبر ساكنات وسيطة، و يلاحظ تكون ممالا لتردد الحليلات يزداد وسعا كلما كبرت المسافة الفاصلة بين الساكنات .
ـ خلاصة:
تمكن الهجرة من:
ـ تغيير البنية الوراثية للساكنات المستقبلة بالرفع من التغير الوراثي عبر وصول حليلات جديدة من ساكنات بعيدة.
ـ التخليط الوراثي بين ساكنات متباعدة مما يؤدي الى تقليص التباين الوراثي بين هذه الساكنات.
9 ـ التطور الضمنوعي: مثال حلزون الخشب Cepaea nemoralis
تساهم عوامل التغير الوراثي للساكنة في تغيير ترددات الحليلات عبر الاجيال مما يساهم في ظهور حليلات جديدة و اختفاء اخرى و انتشار حليلات اخرى،مما يحدث تغيرات على مستوى النوع.
ـ المعايير المميزة للنوع:
لتمييز النوع نعتمد على مجموعة من المعايير التالية:
ـ معايير مورفولوجية
ـ معايير صبغية
ـ معايير بيوكيميائية وراثية
ـ معايير سلوكية
ـ معايير ايكولوجية
ـ معايير فيزيولوجية
ـ معيار الخصوبة:و هو اهم معيار لتحديد النوع و يتجلى في قدرة الافراد على التوالد واعطاء خلف خصيب .
ـ التطور الضمنوعي:
ينتج التطور الصمنوعي عن تعاقب مجموعة من التغيرات الوراثية الصغيرة نسبيا داخل النوع نفسه بحيث لا تؤثر على قدرة الافراد على التوالد و اعطاء خلف خصيب.
ـ خلاصة:
كلما كانت المسافة التي تعزل بين ساكنات من نفس النوع كبيرة الا وكان الاحتمال كبيرا ان تعرف اختلافات في عدد من الخاصيات الوراثية ويرجع ذلك الى تراكم تدريجي لمجموعة من التغيرات الوراثية عبر الزمن نتيجة مجموعة من الاليات(الطفرات، الهجرة، الانتقاء الطبيعي والانحراف الجيني) مع الحفاظ على القدرة على التوالد واعطاء الخلف الخصيب.
EZEL
ردحذف